Dynamic programming examples in life

Dynamic programming is an effective way to solve problems that consist of an optimal substructure and a series of sub-problems. Typically, dynamic programming works more efficiently since it saves results to avoid unnecessary repeated work. Dynamic programming is often used in our daily life. You may even not notice that. From the information at algomonster, you’ll learn something about this technique and its applications in real life.

About dynamic programming (DP)

• It is a well-known method for dealing with problems by dividing them into overlapping sub-problems that shows an optimal substructure.
• Though not precise, you can regard DP as a top-down approach using a bottom-up evaluation. 
• People use dynamic programming to solve optimization-related issues.

How does dynamic programming work?

However helpful this problem-solving approach might be, it can’t solve every problem you encounter. To spot problems that apply to DP, we first should identify the following traits:

• There are the divided sub-problems. Find the solutions to them.
• These smaller sub-problems are interdependent. You only find the solution to a smaller sub based on the solution of the previous even smaller one. This process is referred to as recursion. You will need to use memoization to memorize the results for later use.
• You solve the biggest problem or your original problem by constructing the solutions to all the sub-problems.

Examples of Dynamic programming problems

What is true about the problems tagged online under dynamic programming is that they were formed because of the need for it in reality. Isn’t that the case with other practical techniques? Let’s explore what applications of dynamic programming in real life are like.

Applications in computer science theories

There are a lot of classic DP problems that people analyze in theories. They do this to solve problems that you may meet in real life. Here, we just name several examples of them:

• 0/1 knapsack problem
• All pairs of shortest path problem
• LCS (Longest common subsequence)
• Optimal search binary tree
• Document distance algorithms
• Multistage graph

Applications in real life

Now, let’s see how it works in daily life.

Breaking down Twitter hashtags using the DP method

When you need to break down a Twitter hashtag to categorize a Twitter hashtag, DP could be a great method. Of course, if you ignore the fact that you can split some tags in different ways. That means sometimes it might not always be accurate. The overall accuracy is around 85 percent. To achieve this goal, you need to set a custom scoring function inside the DP, so that the best split is picked based on words’ length and validity. This works perfectly when you have thousands of pieces to deal with. With dynamic programming, you can have it done in just a few seconds. While using brute force, it would take a much longer time.

An example of a Twitter tag: #internationalteachersday

When you input that tag in your DP approach, you’ll get an output: international teachers day. It works for most of the hashtags. 

Other examples of DP solving problems

1. In networking, you can transfer data from a sender to different receivers in a sequential manner. 

2. In Google maps, you can find the shortest path between your home and a number of destinations. Google maps uses the DP algorithm to figure the shortest path between two points.

3. Other aspects such as decision making, economics, connected speech recognition.

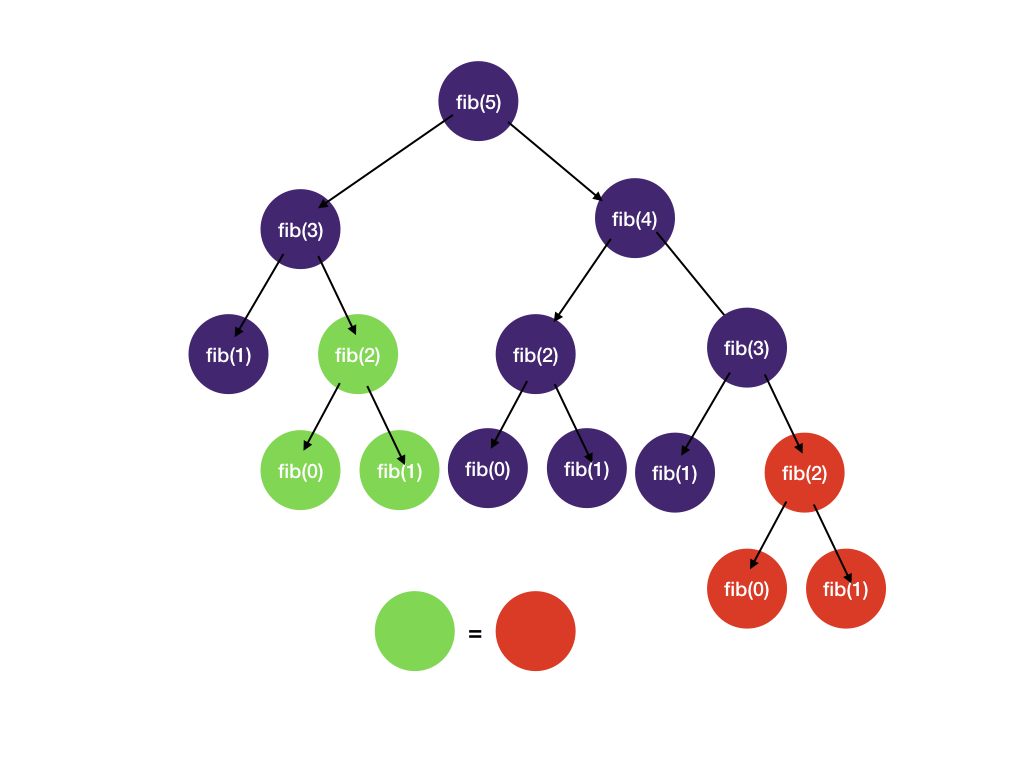
DP questions asked in tech interviews

In many tech interviews, DP is always part of it. There are countless variations in dynamic programming. It is not easy. The interviewers like to find out your ability to solve DP problems. Here are some of the most popular questions you are likely to see in tech interviews.

• Rod cutting
• Partition problem
• Word break problem
• 0/1 knapsack problem
• Coin change problem
• Matrix chain multiplication
• Longest common subsequence
• Shortest common supersequence
• The Levenshtein distance problem
• Longest increasing subsequence problem

Tips for your tech interview dealing with dynamic programming problems

Before the tech interview, you should do the following things.

l Polish your resume. (Highlighting your skills makes your CV convincible.)

l Do thorough research. (Be wise to get fully prepared, it’s vital to know the company you’re going to have the interview with.)

l Practice makes your skills perfect. (Find the information you need, then practice the possible or most commonly seen problems until you master them.)

Steps you need to solve a DP problem

Since you know DP solves a lot of problems, it’s time to understand when you can tackle one with DP. The steps below show you the process using the DP method. It will be useful when you’re in a tech interview as well.

1. Identify that this problem is a DP problem. (Sub-problems and an optimal substructure) 

The first step is essential. You need to make sure this problem can be solved using DP. Otherwise, using DP will only add more burden to your work.

2. Spot the problem variables. (Interconnected sub-problems)

From step one, we know there is a recursive structure between sub-problems. Step two is to see what function parameters are changing. Those parameters normally contain array position and speed.

3. Figure out the recurrence relation inside the problem.

Knowing how sub-problems relate to each other and how you would compute the main problem using the results. 

4. Decide the base sub-problem.

A base sub-problem is one that you can not simplify anymore. In other words, it is the smallest one possible.

5. You have two options to choose from: implement it recursively or iteratively. 

For either of the two methods, you need to decide the base sub-problem and the recurrence relation.

6. Form your table to create memoization so that you will be able to store the results for future reference.

Memoization is a way to memorize previously solved results. When the same inputs appear again, you can reuse the results to save yourself some trouble in recomputing. 

7. Time complexity. (Count the number of states and consider the work done per each state)

Conclusion 

The core principle of dynamic programming is that it is an algorithm that keeps track of the optimal solution to get to every possible state at each step. Then it solves the problem with the combination of these best solutions of the sub-problems. As an optimization-related technique, dynamic programming is widely seen whether it is for computer science, or for daily life applications. Or you’ll need to know more about it before you head for a tech interview.